I nationaløkonomi har man ofte behov for at lave beregninger. Det kan være simple procentberegninger som f.eks. en beregning af danskerens gennemsnitsindkomst i forhold til gennemsnitsamerikanerens.
Hvis danskerens BNP pr indbygger er 30000 dollar pr indbygger og amerikanerens er 40000, så er det altså forholdet 3:4; det samme som 75/100; eller 75 pct (tæller * 100/nævner, eller 3*100/4).
Hvis jeg vil beregne 21 i pct af 87, bruger jeg altså formlen 21*100/87. Det giver 24,14 %. Procentberegninger kan gøre det lettere at sammenligne forskellige tal, da de jo bringes på ens 100-tals formel via procenten.
En anden meget anvendt metode til sammenligning er at bruge indeksberegninger af udvikling i talserier over tid, jvf nedenfor. Herved sætter man et fælles basisår til værdien 100 og beregner ud fra denne grundværdi. Så kan man sammenligne udviklingen for serierne.
Man har ofte behov for at beregne vækst. Hvordan udvikler BNP sig? Formel:
Slutår - begyndelsesår/begyndelsesår * 100. Altså: Slutåret minus begyndelsesåret / divideret med begyndelsesåret. Og det skal ganges med 100. F.eks. ser Danmarks BNP-tal i en kort årrække sådan ud:
| År |
2011 | 2012 | 2013 | 2014 |
| BNP i mia kr |
1833 | 1867 | 1886 | 1921 |
Når jeg nu bruger formlen, så giver det: (1921-1833)*100/1833.
Det bliver 4,8 pct.
- Ikke nogen særlig imponerende økonomisk vækst, men det var i en
periode, hvor Danmark knap nok var kommet ud af finanskrisen endnu.
Og så er tallene oven i købet i "årets priser". Jeg skal
altså trække inflationen fra, hvis jeg skal have den egentlige vækst i
mængder. Det bliver et mindre tal.
Der kommer et mere udbygget eksempel længere nede på siden.
Excel
Den letteste
måde at lave beregninger - og især et antal gentagne beregninger - er
ved at bruge et
elektronisk regneark, f.eks. excel. Princippet for, hvordan man bruger
et regneark, er vist i figuren herunder. Regnearket er inddelt i
rækker (1,2,3,4....) og kolonner (A,B,C,D.....). Det giver et stort
antal celler, hvori der kan tastes talværdier og tekst. Når man vil
lave beregninger, skal man fortælle regnearket, at der arbejdes med
talværdier. Det gøres i Excel ved at sætte = foran i cellen.
Det smarte er, at cellerne kan
referere til hinanden. Det indebærer, at når man har lavet regnearket
med cellereferencer, kan man skifte tallene ud, og så beregnes der med
de nye tal, man sætter ind.
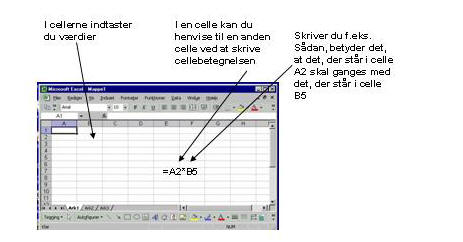 Der
sættes som nævnt lighedstegn foran for at angive, at det er en talværdi, der
arbejdes med. Hvis man nu vil beregne procenten af A2 i procent af B5,
skal man altså skrive: =A2*100/B5. Her fortæller man regnearket, at det,
der står i celle A2 skal ganges med 100, og resultatet heraf skal
divideres med det tal, der tår i celle B5.
Der
sættes som nævnt lighedstegn foran for at angive, at det er en talværdi, der
arbejdes med. Hvis man nu vil beregne procenten af A2 i procent af B5,
skal man altså skrive: =A2*100/B5. Her fortæller man regnearket, at det,
der står i celle A2 skal ganges med 100, og resultatet heraf skal
divideres med det tal, der tår i celle B5.
Denne formel kan kopieres (brug kopier (copy)og sæt ind
(paste) knapperne), så den
anvendes på en række af tal.
Hvis man vil beregne en eksponentiel vækst,
skrives =A2*(1+0,05)n
Det er også det, man kalder "rentes-rente" vækst. Det beregner altså, hvor meget et beløb A2 udvikler sig til i n
perioder og ved en vækstprocent på 5 (se et
eksempel her). Potensophæveren sidder
som regel til højre på
tastaturet og har form af en vinkel med spidsen opad.
Regnearket indeholder funktioner, så man f.eks. kan beregne
annuiteter og
foretage mange andre finansberegninger.
For at bruge denne facilitet går man ind under
indsæt formler og taster funktion. Finansielle og
statistiske funktioner er relevante for samfundsfag. Herefter følger man vejledningen
og taster tallene ind. Når der endelig tastes ok, kommer formlen til at
stå i den celle, hvor cursoren stod.
Regnearket kan bruges til at lave diagrammer i. Du maler et par
talrækker med musen, f.eks. en årstalsrække og en række, der indeholder
den variabel, du vil vise udviklingen for. Derefter
klikkes på diagramikonet i menubjælken. Gå dernæst ned i regnearket og klik med venstre
musetast og "træk" diagrammet ud i det format eller størrelse, du vil have
det;, og man følger dernæst retningslinjerne i diagramwizarden. Til
fortsat redigering kan der klikkes med højre musetast for at fremkalde en
menu, der gør det muligt at ændre de steder i
diagrammet, man vil ændre noget.
Når man arbejder med diagrammet, er det vigtigt at blive klar
over de muligheder, der er for at udforme sit diagram bevidst, så
præsentationen ændrer sig efter de valg, man vil gøre. Man kan f.eks. lave
ændringer af y-aksen, indsætte ekstra y-akse, etc. Hvis man indsætter en
ekstra y-akse, kan man arbejde med visning af kurver for variable med
indbyrdes meget forskellige størrelsesforhold. Hvis man f.eks. vil vise
udviklingen i bruttonationalproduktet (BNP) og sammenholde med rentens
eller inflationens udvikling, så er der jo her tale om talstørrelser, der
er meget forskellige. De små tal ville forsvinde ud af syne, hvis der kun
var én y-akse.
Hvis man arbejder med en variabel, der ændrer sig meget over
tid, eller hvis man arbejder med sammenligning af indbyrdes meget
forskellige talstørrelser, f.eks USA's BNP sammen med Islands, så kan man
vise tallene i et logaritmisk diagram. Man placerer cursoren på y-aksen og
trykker på højre musetast. Herefter kommer en menu frem, så man kan
ændre y-aksens skala til logaritmisk skala.
Man bruger ofte, som nævnt ovenfor, procentberegning for at sammenligne vækst. I økonomisk redegørelse fra Finansministeriet har vi f.eks. følgende tal for Danmarks udenrigshandel:
| Tabel 1: Betalingsbalancens løbende poster i mia kr årets priser | % - ændr. fra 2006 - 2010: | ||||||
| 2006 | 2007 | 2008 | 2009 | 2010 | |||
| Industrieksport ekskl. skibe mv. | 343,6 | 361 | 375,8 | 334,5 | 343,5 | -0,03 | |
| Landbrugseksport mv. | 86,7 | 88,6 | 93,4 | 94,3 | 95,7 | 10,38 | |
| Øvrig vareeksport, ekskl. energi | 38,4 | 33,5 | 39,4 | 40 | 40,6 | 5,73 | |
| Vareeksport ekskl. energi og skibe mv. | 460,9 | 478,3 | 499,2 | 459,3 | 470,1 | 2,00 | |
| Forbrugerprisindeks 2000=100 | 110,4 | 112,4 | 115,7 | 117,8 | ... | ||
| Industrieksport i faste priser | 343,6 | 354,58 | 365,08 | 328,54 | ... | ||
Jeg trækker begyndelsesår fra slutår og beregner forskellen i pct af begyndelsesår for at vise ændringen , f.eks. for landbrugseksporten: (95,7-86,7)*100/86,7 = 10,38%.
For at kunne ræsonnere om betydningen af de økonomiske
sammenhænge er det vigtigt at være klar over, hvad det er, der er blevet
sammenlignet. Læg f.eks. mærke til, at de økonomiske ændringer er i årets
priser.
Hvis vi vil se de virkelige økonomiske ændringer, bør vi trække prisudviklingen fra, så vi får ændringen i volumen, i mængde.
Man deflaterer tallene, dvs renser dem for inflation, ved at dividere med
et
prisindeks. Vi kan finde
prisudviklingen, f.eks.
forbrugerpristallet hos Danmarks Statistik.
Her tager vi altså
forbrugerprisindekset i forhold til år 2000. Tallene kan nu beregnes i
faste priser ved at tallet hvert år divideres med prisindekset det pågældende år
og ganges med indekset i begyndelsesåret.
Det vil sige, at
industrieksporten i faste priser i 2007 i forhold til 2000 er 361*100/114,2 =
?. (Da forbrugerprisindekset jo er steget fra 100 til 114,2 fra 2000
til 2007). Man kan også sige, at man trækker 14,2 pct fra for at få det i faste
priser. (Eksempel på huspriser renset for inflation: Klik
her)
Låse celler til kopiering - Små gyldne tricks med $-tegnet
Den
store fordel med at bruge excel opnår man ved at bruge formler til at
lave mange beregninger med et enkelt tastetryk. Man copy paster sin
formel ud på et større område og laver derved mange beregninger. Da
cellerne flytter sig relativt i forhold til hinanden ved kopieringen,
kan det være nødvendigt at "låse" celler, som der henvises til. Det gør
man ved hjælp af $-dollartegnet på tastaturet.
Jeg vil f.eks. ved hjælp af en indeksberegning lave en undersøgelse af kursudviklingen på nogle vigtige valutaer (klik for at se regnearket) for at se, hvordan deres kursudvikling påvirker dansk økonomi. Hvis det pågældende land er vigtig for dansk eksport, har valutakursudviklingen for landets valuta stor bertydning.
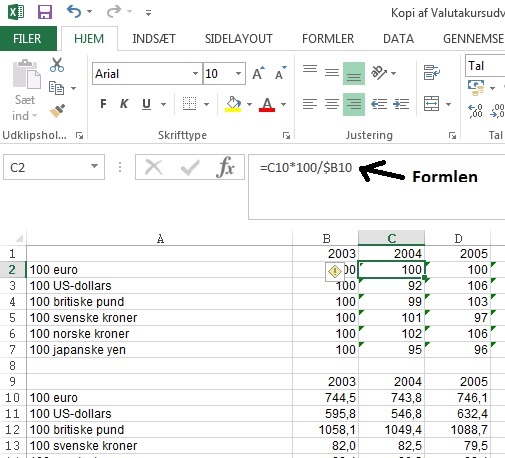
Som det ses af billedet ovenover, er der i formlen øverst indsat et
$-tegn. Det bevirker, at kolonne B fastholdes, når formlen copy pastes,
så der altså holdes fast på tallene i denne kolonne, når der deles. Jeg
starter beregningerne ved at copy paste alle tallene et andet sted hen
i
regnearket, hvorefter der først fastlægges basisværdien 100 i de
kopierede rækker, og hvorefter formlen lægges ind. Nu kan formlen så
kopieres ud i alle rækkerne i de kopierede tal.
På basis af indeksberegningen kan jeg nu lave et diagram, der viser valutakursudviklingen, hvor sammenligningsmulighederne er gode, fordi der startes med samme begyndelsesværdi:
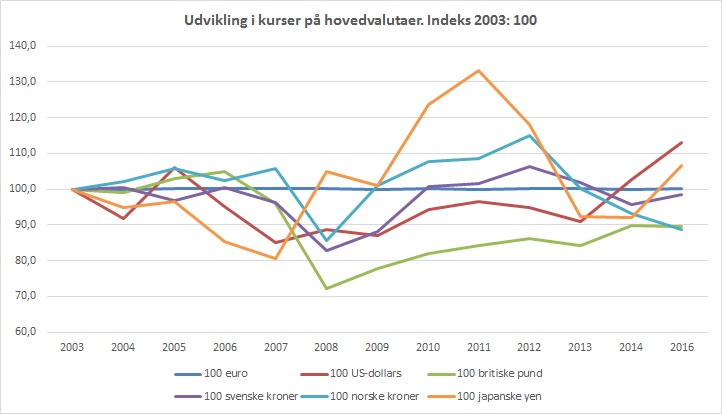
Jeg
har stillet på y-aksen (anbring cursor på aksen og højreklik. der
kommer en menu frem, hvor man kan sættes f.eks. minimumsværdi). Der er
sat minimumsværdi på 60. Derved bliver kurverne tydeligere, så jeg
f.eks. kan se den meget tydelige devaluering af britiske £, som måske
kan være med til at forklare, hvorfor det er gået relativt godt for
Storbritannien efter finanskrisen (genvundet konkurrenceevne via
devaluering). Og der er andre interessante valutariske
udviklingstendenser (dollar, svenske og norske kr).
Når vi
regner relative andele, beregner vi procentvise andele af et ialttal,
f.eks herunder, hvor tre slags indtægter for staten skal beregnes i
procenter, så det ser mere overskueligt ud:
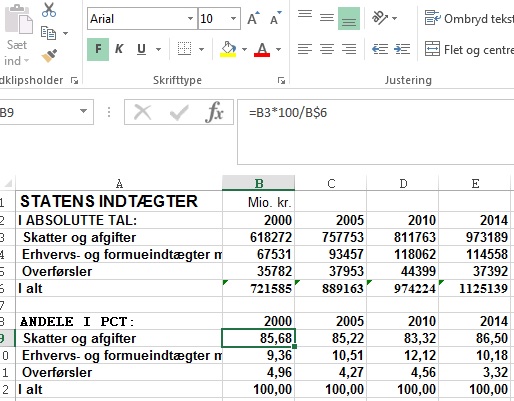
Note: Hent regnearket her.
Den øverste tabel står med absolutte tal i mio. Den copypastes ned, og tallene i den nulstilles. Formlen er sat ind i celle B9, hvor B3 divideres med b6, og der ganges med 100. Række 6 låses fast ved, at der sættes $-tegn foran 6. Denne formel kan nu kopieres ud i tabellen, og procenterne står som ovenfor.
Beregning af udvikling i tidsserie
Udvikling i dansk bistand
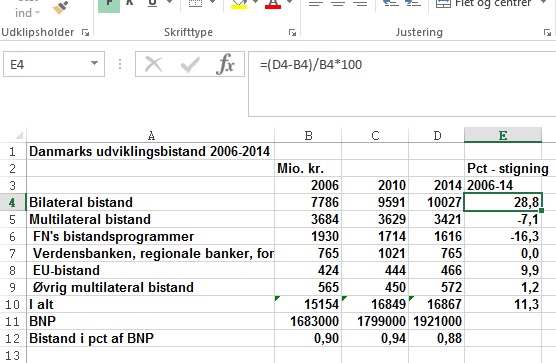
Note: Bilateral: tosidet, dvs fra land til land. Multilateral: flersidet, dvs igennem internationale organisationer som FN eller EU
I
ovenstående tabel er der lavet procentberegning (formlen øverst) for at
vise udviklingen i tallene. Man indsætter en ny kolonne til højre og så
beregner man udviklingen i tallene. Udviklingen i den bilaterale
bistand over perioden beregnes ved, at man tager sidste år, trækker
første år fra og sætter denne difference i procent af første års tal:
(10027-7786)*100/7786). Når der refereres til cellerne (D4-B4)/B4*100,
kan formlen kopieres nedad, og man kan altså lave en ensartet
procentberegning på de talrækker, man er interesseret i. Det vil sige,
man får herved mulighed for at sammenligne udviklingen fra første år
sammenlignet med sidste år. Endvidere er tal for BNP i mio kr sat ind
og bistanden i pct af BNP (B10*100/B11) er beregnet.
Chi2-test
En chi2-test laver vi, når vi har to variable og vil teste, om
forskelligheden mellem dem skyldes en tilfældighed, eller om det er
systematisk. Det kan f.eks. være, hvordan mænd og kvinder stemmer. Der
har vi traditionelt fra vælgerundersøgelser den sammenhæng, at kvinder
gennemgående stemmer mere til venstre end mænd. Det kunne hænge sammen
med en hypotese om, som en amerikansk forfatter har konstateret, at
"kvinder er fra Venus", og "mænd er fra Mars", altså at kvinder stemmer
på partier, der går ind for omsorg og velfærd, mens mænd stemmer på
partier, der går ind for økonomi, erhverv og skattelettelser.
Passer det nu med de seneste valgdata fra Danmark? Det kan undersøges v.h.a. valgdata fra Aalborg universitets Surveybank. Tabellerne herunder viser resultatet:
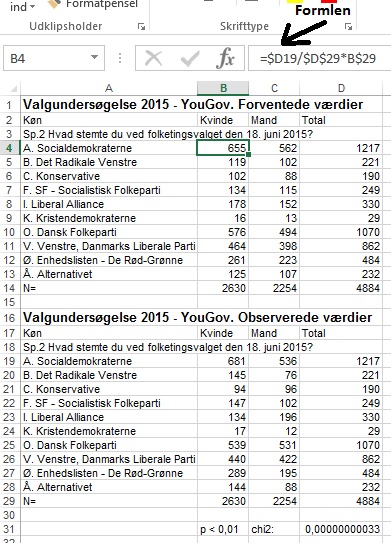
Den nederste tabel viser udtrækket fra surveybankens You Gov undersøgelse fra juni 2015-valget (ved ikke, blanke, mv. er trukket ud). Man ser let på tallene, at kvinderne gennemgående i langt højere grad stemmer rød blok end blå blok (se f.eks. Alternativet og SF i forhold til Liberal Alliance). Men holder det nu, så vi kan sige med en vis sikkerhed, at det ikke kun gælder for de mennesker, der er spurgt i stikprøveundersøgelsen, men også for hele vælgerpopulationen? Det er det, man laver Chi2-undersøgelsen for at finde ud af.
For
at undersøge
det stiller vi en nulhypotese om, at der ikke er nogen sammenhæng. I
øverste tabel er beregnet, hvordan der pr parti ville blive stemt, hvis
det fordelte sig som for hele stikprøven. Formlen i celle B4 er vist
ved pilen. I denne formel er lagt "låse" ind, som fastholder, at der
skal divideres hele vejen igennem med celle B29. Derfor er der sat $
foran både B og 29. $-tegnet angiver absolut cellereference, altså at
der deles alle vegne med denne celle. Der sættes endvidere $ foran
række 29, fordi der skal divideres med den. Og der sættes $ foran
D-kolonnen. Cellen kan nu copypastes ud i hele området, der skal dækkes
af forventede værdier, så der kan sammenholdes med de observerede
værdier. Det gøres v.h.a. formlen for chi2-test, en af de statistiske
formler i excel.
Det viser sig, at
p-værdien bliver under 0,01. Dvs, at sandsynligheden for nulhypotesen,
at der ikke er en sammenhæng, er meget lav. Og der er altså over 99 pct
sandsynlighed for, at der er sammenhængen
mellem køn og partistemme, så vi kan konstatere med stor statistisk
sandsynlighed, at kvinder stemmer mere til venstre end mænd.
Formålet med beregninger: Afdække interessante sammenhænge og problemstillinger
Formålet med beregningerne er at afdække interessante
problemstillinger. Vi får f.eks. figuren over udviklingen i
hovedvalutaers kurser frem ved at lave en indeksberegninger, der sætter
et startår til 100, hvorved vi kan sammenligne ud fra dette
udgangspunkt. Og så få vi interessant resultater frem. Figuren kan
dokumentere en vis sandsynlighed for, at valutaer, der har svinget ned
i kurs efter finanskrisen har bragt de pågældende lande i en stærkere
udenrigsøkonomisk konkurrenceevnesituation. Eller det er i hvert fald
en hypotese, man kan stille, og så forsøge at dokumentere.
Ved hjælp af de beregnede tal i tabellen over udviklingsbistand
ovenover kan vi godtgøre, at Danmark har skiftet fokus i sin
bistandspolitik fra den multilaterale bistand til mere bilateral
bistand, og vi kan se, at udviklingsbistandens andel af BNP er faldende
fra 2010 til 2014.
Andre indeks
Tabel 2 viser det såkaldte nettoprisindeks. Det viser udviklingen i forbrugerpriser, hvor man har trukket virkningen af indirekte skatter (moms og punktafgifter) fra. For at beregne gennemsnitsudviklingen i priserne er man nødt til at tillægge vægte til de forskellige varegrupper i forhold til deres betydning for forbruget. Man bruger en gennemsnitshusholdning som udgangspunkt for tildeling af vægte (procenterne i tabellen). En stigning i fødevarepriserne betyder altså en ottendedel (12,6 pct) betydning for den samlede prisudvikling. Når forbrugets sammensætning ændrer sig, ændres også vægtfordelingen. Fødevarer udgjorde f.eks. en større andel af forbruget tidligere. Med stigende velstand falder fødevarers andel af en gennemsnitsfamilies forbrug.
| Tabel 2: VÆGTE I NETTOPRISINDEKS | |
| Pct. |
Nettopris-
indeks |
| I alt |
100,0
|
| 01. Fødevarer og ikke-alkoholiske drikkevarer |
12,6
|
| 02. Alkoholiske drikkevarer og tobak |
2,5
|
| 03. Beklædning og tøj |
5,2
|
| 04. Bolig |
31,6
|
| 05. Boligudstyr og husholdningstjenester |
6,2
|
| 06. Sundhed |
4,2
|
| 07. Transport |
9,4
|
| 08. Kommunikation |
2,1
|
| 09. Fritid og kultur |
10,3
|
| 10. Uddannelse |
1,0
|
| 11. Restauranter og hoteller |
5,7
|
| 12. Andre varer og tjenester |
9,1
|
|
Anm.: Vægtene
afspejler vægtgrundlaget pr. januar 2003. Kilde: Danmarks Statistik |
|
Det er det samme princip, der bruges ved beregning af aktieindeks. Her tillæges de enkelte aktier vægte efter deres andel af den samlede omsætning på Børsen.
1
Pct-beregning af ændring
Årets priser og faste priser
Pct-andele
Indeksbereg-
ning af tal i seriier
Chi2-test
LINKS:
Kvantitative Metoder uddybende:
Pct-ændringer
Indekstal
Pct-andele
Hvornår pct-ændring og hvornår indeks?
Chi2-testFinansregnere
Bloomberg finansregner (her kan du beregne rentes-rente, annuiteter og meget mere)